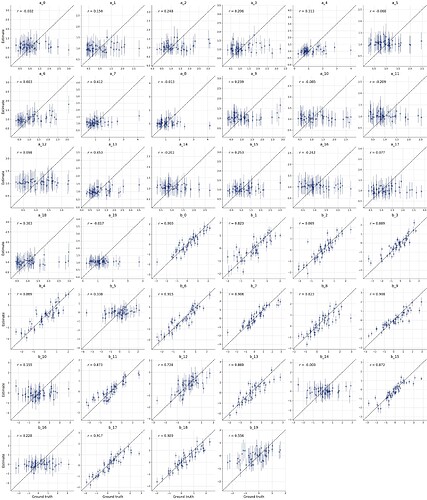
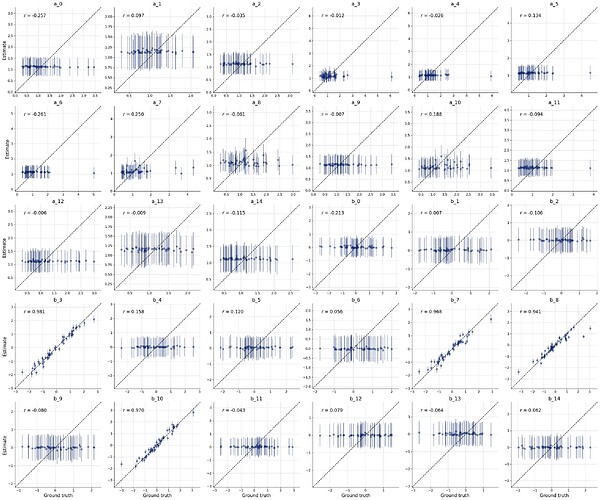
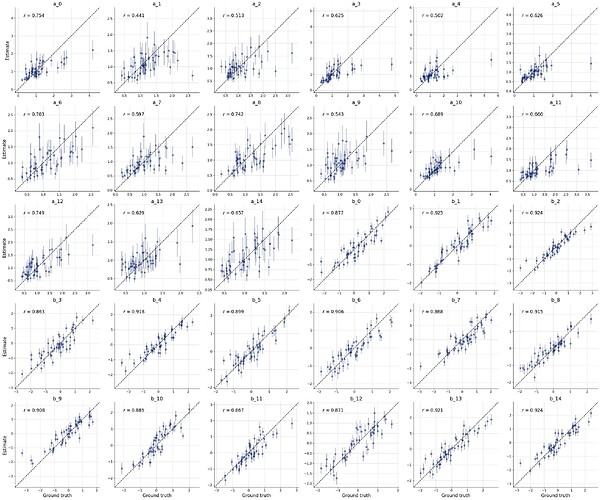
To me this looks somewhat similar to what we have seen in this thread. My guess would be that the summary network cannot handle that much data with its default settings, so it only provides summary statistics for a few variables, and looses the information for the rest. You can try to increase its capacity, but that might be not so straight-forward.
A different approach that I’m currently testing and that seems to be simpler is to just bundle multiple summary networks of the same type to increase the capacity. I have just opened a pull request to make this easier.
Below is a preliminary version if you want to try it out already. Here, the deep set (with the new defaults) seems to work better than the set transfomer.
import os
if "KERAS_BACKEND" not in os.environ:
os.environ["KERAS_BACKEND"] = "tensorflow"
import keras
import bayesflow as bf
import numpy as np
from collections.abc import Mapping, Sequence
from bayesflow.networks import SummaryNetwork
from bayesflow.utils.serialization import deserialize, serializable, serialize
from bayesflow.types import Tensor, Shape
from keras import ops
@serializable("custom")
class InofficialFusionNetwork(SummaryNetwork):
def __init__(
self,
backbones: Sequence | Mapping[str, keras.Layer],
head: keras.Layer | None = None,
**kwargs,
):
"""(SN) Wraps multiple summary networks (`backbones`) to learn summary statistics from (optionally)
multi-modal data.
There are two modes of operation:
- Identical input: each backbone receives the same input. The backbones have to be passed as a sequence.
- Multi-modal input: each backbone gets its own input, which is the usual case for multi-modal data. Networks
and inputs have to be passed as dictionaries with corresponding keys, so that each
input is processed by the correct summary network. This means the "summary_variables" entry to the
approximator has to be a dictionary, which can be achieved using the
:py:meth:`bayesflow.adapters.Adapter.group` method.
This network implements _late_ fusion. The output of the individual summary networks is concatenated, and
can be further processed by another neural network (`head`).
Parameters
----------
backbones : Sequence or dict
Either (see above for details):
- a sequence, when each backbone should receive the same input.
- a dictionary with names of inputs as keys and corresponding summary networks as values.
head : keras.Layer, optional
A network to further process the concatenated outputs of the summary networks. By default,
the concatenated outputs are returned without further processing.
**kwargs
Additional keyword arguments that are passed to the :py:class:`~bayesflow.networks.SummaryNetwork`
base class.
"""
super().__init__(**kwargs)
self.backbones = backbones
self.head = head
self._dict_mode = isinstance(backbones, Mapping)
if self._dict_mode:
# order keys to always concatenate in the same order
self._ordered_keys = sorted(list(self.backbones.keys()))
def build(self, inputs_shape: Shape | Mapping[str, Shape]):
if self._dict_mode and not isinstance(inputs_shape, Mapping):
raise ValueError(
"`backbones` were passed as a dictionary, but the input shapes are not a dictionary. "
"If you want to pass the same input to each backbone, pass the backbones as a list instead of a "
"dictionary. If you want to provide each backbone with different input, please ensure that you have "
"correctly assembled the `summary_variables` to provide a dictionary using the Adapter.group method."
)
if self.built:
return
output_shapes = []
if self._dict_mode:
missing_keys = list(set(inputs_shape.keys()).difference(set(self._ordered_keys)))
if len(missing_keys) > 0:
raise ValueError(
f"Expected the input to contain the following keys: {self._ordered_keys}. "
f"Missing keys: {missing_keys}"
)
for k, shape in inputs_shape.items():
# build each summary network with different input shape
if not self.backbones[k].built:
self.backbones[k].build(shape)
output_shapes.append(self.backbones[k].compute_output_shape(shape))
else:
for backbone in self.backbones:
# build all summary networks with the same input shape
if not backbone.built:
backbone.build(inputs_shape)
output_shapes.append(backbone.compute_output_shape(inputs_shape))
if self.head and not self.head.built:
fusion_input_shape = (*output_shapes[0][:-1], sum(shape[-1] for shape in output_shapes))
self.head.build(fusion_input_shape)
self.built = True
def compute_output_shape(self, inputs_shape: Mapping[str, Shape]):
output_shapes = []
if self._dict_mode:
output_shapes = [self.backbones[k].compute_output_shape(shape) for k, shape in inputs_shape.items()]
else:
output_shapes = [backbone.compute_output_shape(inputs_shape) for backbone in self.backbones]
output_shape = (*output_shapes[0][:-1], sum(shape[-1] for shape in output_shapes))
if self.head:
output_shape = self.head.compute_output_shape(output_shape)
return output_shape
def call(self, inputs: Mapping[str, Tensor], training=False):
"""
Parameters
----------
inputs : Tensor | dict[str, Tensor]
Either (see above for details):
- a tensor, when the backbones where passed as a list and should receive identical inputs
- a dictionary, when the backbones were passed as a dictionary, where each value is the input to the
summary network with the corresponding key.
training : bool, optional
Whether the model is in training mode, affecting layers like dropout and
batch normalization. Default is False.
"""
if self._dict_mode:
outputs = [self.backbones[k](inputs[k], training=training) for k in self._ordered_keys]
else:
outputs = [backbone(inputs, training=training) for backbone in self.backbones]
outputs = ops.concatenate(outputs, axis=-1)
if self.head is None:
return outputs
return self.head(outputs, training=training)
def compute_metrics(self, inputs: Mapping[str, Tensor], stage: str = "training", **kwargs) -> dict[str, Tensor]:
"""
Parameters
----------
inputs : Tensor | dict[str, Tensor]
Either (see above for details):
- a tensor, when the backbones where passed as a list and should receive identical inputs
- a dictionary, when the backbones were passed as a dictionary, where each value is the input to the
summary network with the corresponding key.
stage : bool, optional
Whether the model is in training mode, affecting layers like dropout and
batch normalization. Default is False.
**kwargs
Additional keyword arguments.
"""
if not self.built:
self.build(keras.tree.map_structure(keras.ops.shape, inputs))
metrics = {"loss": [], "outputs": []}
def process_backbone(backbone, input):
# helper function to avoid code duplication for the two modes
if isinstance(backbone, SummaryNetwork):
backbone_metrics = backbone.compute_metrics(input, stage=stage, **kwargs)
metrics["outputs"].append(backbone_metrics["outputs"])
if "loss" in backbone_metrics:
metrics["loss"].append(backbone_metrics["loss"])
else:
metrics["outputs"].append(backbone(input, training=stage == "training"))
if self._dict_mode:
for k in self._ordered_keys:
process_backbone(self.backbones[k], inputs[k])
else:
for backbone in self.backbones:
process_backbone(backbone, inputs)
if len(metrics["loss"]) == 0:
del metrics["loss"]
else:
metrics["loss"] = ops.sum(metrics["loss"])
metrics["outputs"] = ops.concatenate(metrics["outputs"], axis=-1)
if self.head is not None:
metrics["outputs"] = self.head(metrics["outputs"], training=stage == "training")
return metrics
def get_config(self) -> dict:
base_config = super().get_config()
config = {
"backbones": self.backbones,
"head": self.head,
}
return base_config | serialize(config)
@classmethod
def from_config(cls, config: dict, custom_objects=None):
config = deserialize(config, custom_objects=custom_objects)
return cls(**config)
# Set seeds for reproducibility
np.random.seed(42)
# Global parameters
N_ITEMS = 20
N_PERSONS = 400
SUMMARY_DIM = (N_ITEMS * 2) * 4 # number of summary dimensions used for summary networks in total
NUM_SUMMARY_NETWORKS = 4 # number of summary networks (SetTransformer)
NUM_COUPLING_LAYERS = 3 # number of coupling layers used for inference network (CouplingFlow)
EPOCHS = 10
BATCH_SIZE = 16
NUM_BATCHES_PER_EPOCH = 1000
# Create simulator
def prior(n_items):
a = np.random.lognormal(0, 0.5, size=n_items) # discrimination
b = np.random.normal(0, 1, size=n_items) # difficulty
return dict(a=a, b=b)
def likelihood(a, b, n_persons):
"""Likelihood function generating response data"""
theta = np.random.normal(0, 1, size=n_persons)
linear_predictors = a[:, None] * (theta[None, :] - b[:, None])
p = 1 / (1 + np.exp(-linear_predictors))
responses = np.random.binomial(1, p)
responses = responses.swapaxes(-1, -2)
return dict(theta = theta, responses=responses)
def meta():
return dict(n_items = N_ITEMS, n_persons = N_PERSONS)
simulator = bf.make_simulator([prior, likelihood], meta_fn=meta)
# Create adapter
adapter = (
bf.adapters.Adapter()
.to_array()
.constrain("a", lower=0.01) # discrimination must be positive
.convert_dtype(from_dtype="float64", to_dtype="float32")
.broadcast("n_items", to="a")
.broadcast("n_persons", to="theta")
.concatenate(["n_items", "n_persons"], into="inference_conditions")
.rename("responses", "summary_variables")
.concatenate(["a", "b"], into="inference_variables")
)
# Test simulator and adapter
test_data = simulator.sample(2)
print(f"Simulator output shapes:")
for key, value in test_data.items():
if hasattr(value, 'shape'):
print(f" {key}: {value.shape}")
else:
print(f" {key}: {value}")
adapted_data = adapter(test_data)
print(f"\nAdapter output shapes:")
for key, value in adapted_data.items():
if hasattr(value, 'shape'):
print(f" {key}: {value.shape}")
else:
print(f" {key}: {value}")
# Define networks
summary_network = InofficialFusionNetwork(
backbones=[
bf.networks.DeepSet(summary_dim=SUMMARY_DIM // NUM_SUMMARY_NETWORKS, mlp_widths_invariant_outer=(64, 4))
for _ in range(NUM_SUMMARY_NETWORKS)
]
)
inference_network = bf.networks.CouplingFlow(num_coupling_layers=NUM_COUPLING_LAYERS)
# Create workflow
workflow = bf.BasicWorkflow(
simulator=simulator,
adapter=adapter,
inference_network=inference_network,
summary_network=summary_network,
)
validation_data = simulator.sample(500)
# Train model
history = workflow.fit_online(
epochs=EPOCHS,
batch_size=BATCH_SIZE,
num_batches_per_epoch=NUM_BATCHES_PER_EPOCH,
validation_data=validation_data,
)
bf.diagnostics.plots.loss(history)
# Test parameter recovery
result = workflow.sample(conditions=validation_data, num_samples=50)
bf.diagnostics.plots.recovery(
estimates=result,
targets=validation_data
)
This gives the following result: