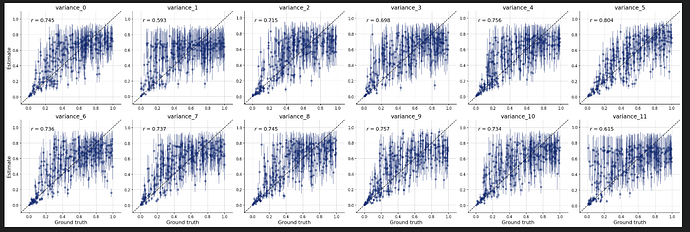
Does it make any difference whether or not inputs are standardized?
It didn’t make any difference for me whether it was standardised or not.
I believe the problem is that there is nothing interesting to learn from the data except the empirical variance and the prior variance. All computations in the transformer are then focused at simply copying the data and computing the variance for each of the independent axes. I will try to find out why this is hard for permutation-invariant networks in a bit. The same goes for not using a summary net and relying on the internal networks. Nets seem to be much better at learning dependencies than independencies.
To prove the point, here is a summary network with a proper inductive bias that easily solves Valentin’s case (i.e., simply repeats the same invariant op across each axis → doesn’t need to learn to do it):
class CustomSummary(bf.networks.SummaryNetwork):
def __init__(self, deep_set_dim=4, **kwargs):
super().__init__(**kwargs)
self.deep_set = bf.networks.DeepSet(summary_dim=deep_set_dim)
self.deep_set_dim = deep_set_dim
self.summary_stats = keras.layers.Dense(8)
def call(self, x, **kwargs):
"""Will apply the same deep set across each axis 1,...,D."""
shape = keras.ops.shape(x)
B, _, D = shape[0], shape[1], shape[2]
x = keras.ops.swapaxes(x, axis1=1, axis2=2)[..., None]
summary = self.deep_set(x, training=kwargs.get("stage") == "training")
summary = keras.ops.reshape(summary, (B, D*self.deep_set_dim))
summary = self.summary_stats(summary)
return summary
The lesson is the usual deep learning mantra → inductive bias is important. I am not sure there is a general solution to this in SBI, since the summary network (or the network backbone) needs to be aligned with the symmetry of the data. I still think that learning large covariance matrices is an interesting challenge tho.
PS. I think @valentin had a similar (more general version of this) network in the previous version. Perhaps we should revive it?
Ok, so just to be sure i’m following:
Would that suggest the nets should be able to solve my original problem with dependencies in the covariance structure? Or is the contention now that the current workflows (nets or without nets) can’t handle the estimation of covariance structures well?
I would say in theory the transformer with its self-attention mechanism should be a good enough summary net, given a sufficient number of simulations. Of course, NUTS will have a tremendous advantage for this case, since it’s likelihood-based.
I have never tried estimating covariance matrices with bayesflow before, but I can imagine that there may be a better way to summarize data for such symmetric, pairwise-dependence problems and this thread can make a contribution to a better understanding of the problem.
Thanks for your help folks! Appreciate you digging in!
Hi folks,
Thought i’d follow up here just in case of interest. I thought the discussion above interesting enough that i wanted to interrogate the notion of inductive bias further in deep-learning architectures a bit further.
So I wrote up a comparison of Variational Auto-encoder model specifications with simpler Bayesian estimation.I know VAEs aren’t the same thing as Amortized Bayesian architectures, but i had a better handle on how to implement VAEs… and i guess the inductive biases problem extends to Amotized bayesian architectures too.
I was able to find both (a) a VAE architecture that can recover the latent correlation structure if scaled up with enough data and (b) a theoretically superior architecture designed to handle missing data that breaks on the reconstruction task when trying to do so.
Both are then compared to the simpler multivariate normal Bayesian model in PyMC which is able to recover the correlation structure much more efficiently.
I draw some lessons about the value of transparent inductive biases, but would love to hear any feedback or pushback.
Anyway, thanks for the stimulating work!
Blog link: Heuristics in Latent Space: VAEs and Bayesian Inference – Examined Algorithms
Very cool blog post! Thank you for sharing ![]()